SVMs Dual Formulation
Background
Support Vector Machines (SVMs) are a powerful and versatile class of supervised learning models used for classification and regression tasks. They are particularly known for their ability to handle complex, non-linear decision boundaries.
We have seen the primal and dual formulations of the linear SVM elsewhere. We often use the dual form with SGD to solve the SVM problem. Here I will derive the dual formulation of the hard margin SVM and soft margin SVM step by step. Basically is using Lagrange duality and KKT condition.
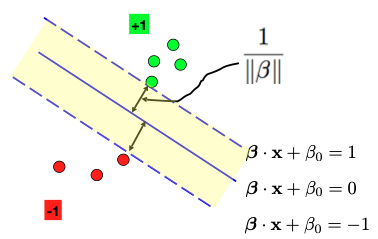
(Linear separable case of SVM. Source: [1])
Lagrange Duality
First, we have the constraint optimization problem with equality and inequality constraints [2]:
\[\begin{align*} \min_{w} \quad & f(w) \\ \text{s.t.} \quad & g_i(w) \leq 0, \quad i = 1, 2, \ldots, n \\ \text{s.t.} \quad & h_j(w) = 0, \quad j = 1, 2, \ldots, m \end{align*}\]Using the method of Lagrange multipliers, the Lagrangian is [2]:
\[\mathcal{L}(w, \alpha, \beta) = f(w) + \sum_{i=1}^n \alpha_i g_i(w) + \sum_{j=1}^m \beta_j h_j(w)\]where $\alpha_i$ are the Lagrange multipliers for the inequality constraints, and $\beta_j$ are the Lagrange multipliers for the equality constraints.
The Dual and Primal are related by [2]:
\[d^* = \max_{\alpha, \beta : \alpha_i \geq 0} \min_{w} \mathcal{L}(w, \alpha, \beta) \leq \quad p^* = \min_{w} \max_{\alpha, \beta : \alpha_i \geq 0} \mathcal{L}(w, \alpha, \beta)\]where $d^*$ is the dual optimal and $p^*$ is the primal optimal.
KKT Condition
Base on the above dual primal relation, and under some conditions, the dual optimal is equal to the primal optimal $d^* = p^*$. Suppose f and g are convex, and h is affine, then the KKT conditions are:
\[\begin{align*} \frac{\partial}{\partial w_i} \mathcal{L}(w^*, \alpha^*, \beta^*) & = 0, \quad i = 1, 2, \ldots, m \\ \frac{\partial}{\partial \beta_j} \mathcal{L}(w^*, \alpha^*, \beta^*) & = 0, \quad j = 1, 2, \ldots, l \\ \alpha_i^* g_i(w^*) & = 0, \quad i = 1, 2, \ldots, k \quad \text{(Complementary Slackness)} \\ g_i(w^*) & \leq 0, \quad i = 1, 2, \ldots, k \quad \text{(Primal Feasibility)} \\ \alpha_i^* & \geq 0, \quad i = 1, 2, \ldots, k \quad \text{(Dual Feasibility)} \\ \end{align*}\]with the first two conditions being the stationary conditions, and the last three being the feasibility conditions.
Hard Margin SVM
Primal form of hard margin SVM:
\[\begin{align*} \min_{w, b} \quad & \frac{1}{2} \|w\|^2_2 \\ s.t. \quad & y^{(i)} (w^T x^{(i)} + b) \geq 1, \quad i = 1, 2, \ldots, n \end{align*}\]The Lagrangian function with Lagrange multipliers $\alpha_i \geq 0$ is:
\[\mathcal{L}(w, b, \alpha) = \frac{1}{2} \|w\|^2_2 + \sum_{i=1}^n \alpha_i (1 - y^{(i)} (w^T x^{(i)} + b))\]To minimize $\mathcal{L}(w, b, \alpha)$ w.r.t. $w$ and $b$, we get:
\[\begin{align*} \frac{\partial}{\partial w} \mathcal{L}(w, b, \alpha) & = w - \sum_{i=1}^n \alpha_i y^{(i)} x^{(i)} = 0 \\ \implies w & = \sum_{i=1}^n \alpha_i y^{(i)} x^{(i)} \qquad \text{(1)} \\ \frac{\partial}{\partial b} \mathcal{L}(w, b, \alpha) & = \sum_{i=1}^n \alpha_i y^{(i)} = 0 \qquad \text{(2)} \end{align*}\]Substituting (1) and (2) into $\mathcal{L}(w, b, \alpha)$, we get:
\[\begin{align*} \mathcal{L}(w, b, \alpha) & = \frac{1}{2} \left( \sum_{i=1}^n \alpha_i y^{(i)} x^{(i)} \right)^\top \left( \sum_{i=1}^n \alpha_i y^{(i)} x^{(i)} \right) + \sum_{i=1}^n \alpha_i - \sum_{i=1}^n \alpha_i y^{(i)} \left( \sum_{j=1}^n \alpha_j y^{(j)} x^{(j)} \right)^\top x^{(i)} - \sum_{i=1}^n \alpha_i y^{(i)} b \\ & = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y^{(i)} y^{(j)} x^{(i)\top} x^{(j)} \\ \end{align*}\]With dual feasibility condition $\alpha_i \geq 0$, we have the following dual optimization problem:
\[\begin{align*} \max_{\alpha} \quad & \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y^{(i)} y^{(j)} x^{(i)\top} x^{(j)} \\ s.t. \quad & \sum_{i=1}^n \alpha_i y^{(i)} = 0 \\ & \alpha_i \geq 0, \quad i = 1, 2, \ldots, n \end{align*}\]Soft Margin SVM
For non-linearly seperable case, we can use soft margin SVM by introducing slack variables $\xi_i \geq 0$. We add a regularization term to the objective function to make it less sensitive to outliers.
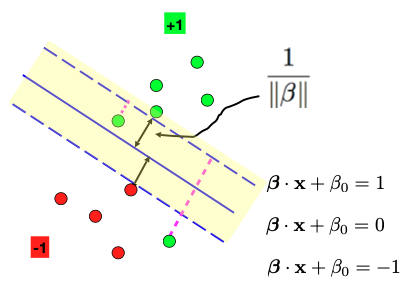
(Non-linear separable case of SVM. Source: [1])
L1 Regularization
Objective function with L1 regularization:
\[\begin{align*} \min_{w, b, \xi} \quad & \frac{1}{2} \|w\|^2_2 + C \sum_{i=1}^n \xi_i \\ s.t. \quad & y^{(i)} (w^T x^{(i)} + b) \geq 1 - \xi_i\\ & \xi_i \geq 0, \quad \forall i \in \{1, 2, \ldots, N\} \end{align*}\]The Lagrangian function with Lagrange multipliers $\alpha_i \geq 0$ and $\mu_i \geq 0$ is:
\[\begin{align*} L(w, b, \xi, \alpha, \beta) & = \frac{1}{2} \|w\|_2^2 + C \sum_{i=1}^{N} \xi_i - \sum_{i=1}^{N} \alpha_i \left( y^{(i)} \left( w^\top x^{(i)} + b \right) - 1 + \xi_i \right) - \sum_{i=1}^{N} \beta_i \xi_i \\ & = \frac{1}{2} \|w\|_2^2 + \sum_{i=1}^{N} \alpha_i \left( 1 - y^{(i)} \left( w^\top x^{(i)} + b \right) \right) - \sum_{i=1}^{N} ( C - \alpha_i - \beta_i ) \xi_i \end{align*}\]To minimize $\mathcal{L}(w, b, \xi, \alpha, \beta)$ w.r.t. $w$, $b$, and $\xi$, we get:
\[\begin{align*} \frac{\partial L}{\partial w} & = 0 \implies w = \sum_{i=1}^{N} \alpha_i y^{(i)} x^{(i)} \\ \frac{\partial L}{\partial b} & = 0 \implies \sum_{i=1}^{N} \alpha_i y^{(i)} = 0 \\ \frac{\partial L}{\partial \xi} & = 0 \implies C - \alpha_i - \beta_i = 0 \end{align*}\]with the following feasibility conditions:
\[\begin{align*} \text{Primal feasibility} & \quad y^{(i)} \left( w^\top x^{(i)} + b \right) \geq 1 - \xi_i, \quad \xi_i \geq 0 \\ \text{Dual feasibility} & \quad \alpha_i \geq 0, \quad \beta_i \geq 0 \\ \text{Complementary slackness} & \quad \alpha_i \left( 1 - \xi_i - y^{(i)} \left( w^\top x^{(i)} + b \right) \right) = 0, \quad \beta_i \xi_i = 0 \end{align*}\]Substituting the partial derivatives result into the Lagrangian function, and using the dual form of hard margin SVM, we obtain the dual form for soft margin SVM with L1 regularization:
\[\begin{align*} \max_{\alpha \geq 0} & \quad \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} x^{(i) \top} x^{(j)} \\ \text{s.t.} & \quad \sum_{i=1}^{N} \alpha_i y^{(i)} = 0, \quad C \geq \alpha_i \geq 0, \quad \forall i \in \{1, \ldots, N\}. \end{align*}\]L2 Regularization
Objective function with L2 regularization:
\[\begin{align*} \arg\min_{w, b, \xi} & \quad \frac{1}{2} \|w\|_2^2 + \frac{C}{2} \sum_{i=1}^{N} \xi_i^2 \\ \text{s.t.} & \quad y^{(i)} \left( w^\top x^{(i)} + b \right) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad \forall i \in \{1, \ldots, N\}. \end{align*}\]Similar to the L1 regularization, we obtain the Lagrangian function with Lagrange multipliers $\alpha$ and $\beta$:
\[\begin{align*} L(w, b, \xi, \alpha, \beta) & = \frac{1}{2} \|w\|_2^2 + \frac{C}{2} \sum_{i=1}^{N} \xi_i^2 - \sum_{i=1}^{N} \alpha_i \left( y^{(i)} \left( w^\top x^{(i)} + b \right) - 1 + \xi_i \right) - \sum_{i=1}^{N} \beta_i \xi_i \\ & = \frac{1}{2} \|w\|_2^2 + \sum_{i=1}^{N} \alpha_i \left( 1 - y^{(i)} \left( w^\top x^{(i)} + b \right) \right) - \sum_{i=1}^{N} \xi_i( \frac{C}{2}\xi_i - (\alpha_i + \beta_i )) \end{align*}\]To minimize $\mathcal{L}(w, b, \xi, \alpha, \beta)$ w.r.t. $w$, $b$, and $\xi$, we get:
\[\begin{align*} \frac{\partial L}{\partial w} & = 0 \implies w = \sum_{i=1}^{N} \alpha_i y^{(i)} x^{(i)} \\ \frac{\partial L}{\partial b} & = 0 \implies \sum_{i=1}^{N} \alpha_i y^{(i)} = 0 \\ \frac{\partial L}{\partial \xi} & = 0 \implies C \xi_i = \alpha_i + \beta_i \end{align*}\]With the following feasibility conditions:
\[\begin{align*} \text{Primal feasibility} & \quad y^{(i)} \left( w^\top x^{(i)} + b \right) \geq 1 - \xi_i, \quad \xi_i \geq 0 \\ \text{Dual feasibility} & \quad \alpha_i \geq 0, \quad \beta_i \geq 0 \\ \text{Complementary slackness} & \quad \alpha_i \left( 1 - \xi_i - y^{(i)} \left( w^\top x^{(i)} + b \right) \right) = 0, \quad \beta_i \xi_i = 0 \end{align*}\]By complementary slackness conditions, when $\xi_i > 0$, $\beta_i = 0$, we then have $C \xi_i = \alpha_i$.
Substituting the partial derivatives result into the Lagrangian function, and using the dual form of hard margin SVM, we obtain the dual form for soft margin SVM with L2 regularization:
\[\begin{align*} \max_{\alpha \geq 0} & \quad \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} x^{(i) \top} x^{(j)} - \frac{1}{2} \sum_{i=1}^{N} \frac{\alpha_i^2}{C} \\ \text{s.t.} & \quad \sum_{i=1}^{N} \alpha_i y^{(i)} = 0, \quad C \geq \alpha_i \geq 0, \quad \forall i \in \{1, \ldots, N\}. \end{align*}\]SVM Solver in Python
Python code to solve the hard margin SVM and soft margin SVM with L1 regularization.
def svm_solver(x_train, y_train, lr, num_iters, c=None):
'''
Arguments:
x_train: 2d tensor with shape (N, d).
y_train: 1d tensor with shape (N,), whose elememnts are +1 or -1.
lr: The learning rate.
num_iters: The number of gradient descent steps.
c: The trade-off parameter in soft-margin SVM.
The default value is None, referring to the basic, hard-margin SVM.
Returns:
alpha: a 1d tensor with shape (N,), denoting an optimal dual solution.
Initialize alpha to be 0.
'''
N = x_train.shape[0]
alpha = torch.zeros(N, requires_grad=True)
# compute kernel matrix
K = x_train @ x_train.T
yi_yj_K = torch.outer(y_train, y_train) * K
for _ in range(num_iters):
# dual objectives
obj = alpha.sum() - 0.5 * alpha @ yi_yj_K @ alpha
# compute the gradient of the dual objectives
obj.backward()
# update the alpha with gradient descent / ascent
with torch.no_grad():
alpha += lr * alpha.grad
# projected gradient
if c is not None:
# soft margin SVM
alpha.clamp_(0, c)
else:
# hard margin SVM
alpha.clamp_(0)
alpha.grad.zero_()
return alpha.detach()
References
[1] UIUC CS598 Practical Statistical Learning Chapter 11 Support Vector Machines. John Marden, Feng Liang. Link: https://liangfgithub.github.io/PSL/w11/w11_1_separable_case.html
[2] Stanford CS229 Machine Learning Main notes. Andrew Ng, Tengyu Ma. Link: https://cs229.stanford.edu/main_notes.pdf
tags: Machine LearningBack to Blogs | Top | Tags