Movie Recommendation with Item-based Collaborative Filtering
Background
I have completed the CS598 Practical Statistical Learning course last semester (2024 Fall). This course covers the basic concepts of statistical learning, including linear models, non-linear models, and ensemble methods. The last project of the course is to build a movie recommendation system using item-based collaborative filtering (IBCF). It is quite a fun project to implement from algorithm to deployment on web.
- Website: Streamlit App
- Code: Github
- Course material: PSL textbook
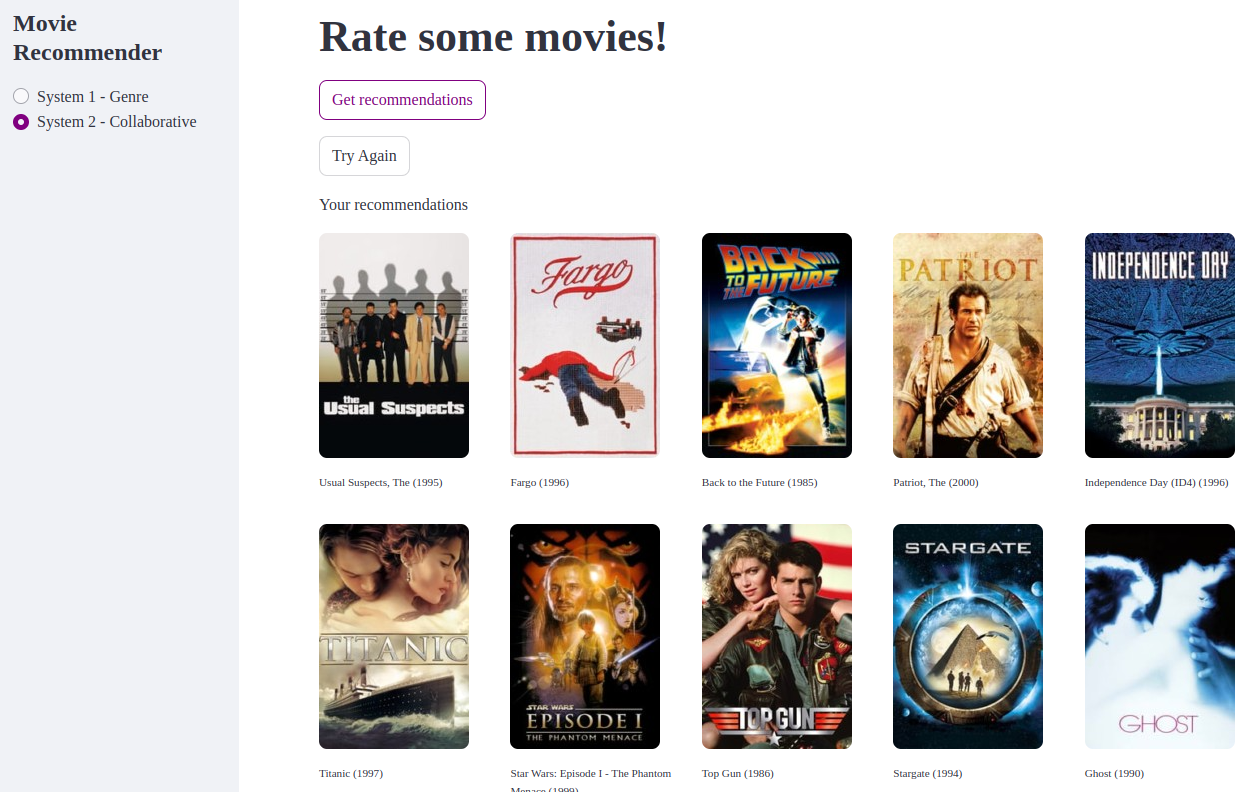
Item-based Collaborative Filtering
The project used the MovieLens Dataset with ~1 million anonymous ratings for 3,706 movies, provided by 6,040 MovieLens users who joined the platform in 2000.
Matrix variables used for the project and their dimensions:
- $\mathbf{R}$: denote the 6040-by-3706 user-movie rating matrix.
- $\mathbf{S}$: denote the 3706-by-3706 similarity matrix.
- $\mathbf{I}$: denote the 3706-by-3706 cardinality matrix.
We first compute the (transformed) Cosine similarity among the 3,706 movies. For movies $i$ and $j$, let \(\mathcal{I}_{ij}\) denote the set of users who rated both movies $i$ and $j$. We ignore similarities computed based on less than three user ratings. Thus, define the similarity between movie $i$ and movie $j$ as follows, when the cardinality of \(\mathcal{I}_{ij}\) is bigger than two,
\[S_{ij} = \frac{1}{2} + \frac{1}{2} \frac{\sum_{l \in \mathcal{I}_{ij}} R_{li}{R_{lj}}}{\sqrt{\sum_{l \in \mathcal{I}_{ij}} R_{li}^2} \sqrt{\sum_{l \in \mathcal{I}_{ij}} R_{lj}^2}}\]Python code to compute the similarity matrix.
def compute_cos_similarity(rating: pd.DataFrame, cardinality: pd.DataFrame):
# recenter the rating matrix
R = rating.subtract(rating.mean(axis=1), axis='rows').fillna(0)
# compute the dot product
dot_product = R.T @ R
# compute the euclidean distance
euclidean_dist = (R.T ** 2) @ (R != 0)
euclidean_dist = euclidean_dist.apply(np.vectorize(np.sqrt))
euclidean_dist = euclidean_dist.T * euclidean_dist
# compute the cosine similarity
cosine_similarity = dot_product / euclidean_dist
# transformed Cosine similarity (1 + cos)/2 ensures the similarity is between 0 and 1
S = (1 + cosine_similarity) / 2
# set the diagonal to nan
np.fill_diagonal(S.values, np.nan)
# ignore similarities computed based on less than three user ratings
S[cardinality < 3] = None
return S
Display the similarity matrix for the selected movies.
movies_ids = ["m1", "m10", "m100", "m1510", "m260", "m3212"]
display(similarity.loc[movies_ids, movies_ids])
| m1 | m10 | m100 | m1510 | m260 | m3212 | |
|---|---|---|---|---|---|---|
| m1 | NaN | 0.512106 | 0.392000 | NaN | 0.741597 | NaN |
| m10 | 0.512106 | NaN | 0.547458 | NaN | 0.534349 | NaN |
| m100 | 0.392000 | 0.547458 | NaN | NaN | 0.329694 | NaN |
| m1510 | NaN | NaN | NaN | NaN | NaN | NaN |
| m260 | 0.741597 | 0.534349 | 0.329694 | NaN | NaN | NaN |
| m3212 | NaN | NaN | NaN | NaN | NaN | NaN |
Then we need to create a function named myIBCF, which takes a newuser a 3706-by-1 vector and similarity matrix as input, and output the top ten movies to this new use using the following formula as the prediction for movie 𝑖:
\[\frac{1}{\sum_{j \in S(i) \cap \{l: w_l \ne NA\}} S_{ij}} \sum_{j \in S(i) \cap \{l: w_l \ne NA\}} S_{ij} w_{j}\]The prediction is missing if the set \(S(i) \cap \{l: w_l \ne NA\}\) is empty, meaning if none of the similar items have been rated by the user.
Here’s the Python code to implement the myIBCF function.
def myIBCF(newuser: pd.Series, similarity: pd.DataFrame) -> pd.Series:
n = 10 # default number of recommendations
w = newuser
S = similarity.fillna(0)
# compute the movie recommendations
rated_movies = w[w.notna()].index
rated_matrix = (~w.isna()).astype(int)
w = w.fillna(0)
recomendations = S.dot(w) / S.dot(rated_matrix)
recomendations = recomendations.sort_values(ascending=False)[0:n].dropna()
return recomendations
Back to Blogs | Top | Tags