Shared-Control Surgical Drilling Robot
Background
This is a project I did for the 2022 Surgical Robot Challenge and other related publications. The objective was to design a shared-control robot platform with a articulated drill as the end-effector for a surgical application. The optimization-based control framework was implemented such that A) the framework is generalizable to different robot platforms and B) the framework can be used to generate a shared-control interface for the robot with linear constraints to incorporate subtasks like collision and singularity avoidance.
Acknowledgements: The project was done under the supervision of Dr. Yan Wang, Dr. Chen Song, Prof Samel KW Au, and Prof. Russell H. Taylor.
Control Framework
Admittance Control
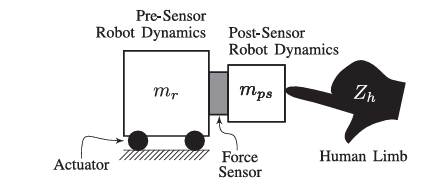
(Generic system diagram of an admittance controlled device. Source: [1])
The transfer function of the robot given as:
\[H(s) = \frac{v(s)}{f(s)} = \frac{1}{M s + B}\]where $v(s) \in \mathbb{R}^6$ is the velocity of the device, $f(s) \in \mathbb{R}^6$ is input force applied by the user, $M \in \mathbb{R}^{6 \times 6}$ is the inertia of the device, and $B \in \mathbb{R}^{6 \times 6}$ is the damping coefficient.
The added small damping term adds phase lead at lower frequencies. It is particularly useful for the robot to have a better tracking performance at low frequencies when the volocity controller bandwidth is low or has long delays [1].
Convex Optimization
Recall the convex quadratic objective and linear constraints setup, where $\dot{q} \in \mathbb{R}^n$ is the joint velocity of the robot with $n$ degrees of freedom:
\[\begin{align*} \min_{\dot{q}} \quad & f_0(\dot{q}) = \frac{1}{2} \dot{q}^\top Q \dot{q} + C^\top \dot{q} \\ \text{subject to} \quad & A_{\text{eq}} \dot{q} = b_{\text{eq}} \\ & A \dot{q} \leq b \end{align*}\]We setup the objective function for task space velocity control with a desired velocity $\dot{x}$ as minimizing the residual between the task space velocity and the desired velocity. The 2-norm of the desired velocity is a constant term and can be ignored for optimization.
\[\begin{align*} f_r(\dot{q}) &= \frac{1}{2} \| J \dot{q} - \dot{x} \|_2^2 - \frac{1}{2} \| \dot{x} \|_2^2 \\ &= \frac{1}{2} \left( J \dot{q} - \dot{x} \right)^\top \left( J \dot{q} - \dot{x} \right) - \frac{1}{2} \dot{x}^\top \dot{x} \\ &= \frac{1}{2} \dot{q}^\top \left( J^\top J \right) \dot{q} + (-v^\top J) \dot{q} \end{align*}\]We can further add a regularization on the joint velocity to smooth the motion:
\[f_j(\dot{q}) = \frac{1}{2} \|\dot{q}\|^2_2 = \frac{1}{2} \dot{q}^\top I_{6\times 6} \dot{q}\]The overall objective function is then:
\[\begin{align*} f(\dot{q}) &= f_r(\dot{q}) + \lambda f_j(\dot{q}) \\ &= \frac{1}{2} \dot{q}^\top \left( J^\top J + \lambda I_{6\times 6} \right) \dot{q} + (-v^\top J) \dot{q} \end{align*}\]with $\lambda$ being the hyperparameter that balances the residual and the regularization.
Equality Constraints
By controlling the equality constraints, we can control the degree of freedom of the end-effector in task space with:
\[\begin{align*} A_{\text{eq}} \dot{q} &= b_{\text{eq}} \\ (S^\top J) \dot{q} &= 0_{6 \times 1} \text{or} = e_{6 \times 1} \\ \end{align*}\]where $v_{qp} = J \dot{q}$ is the task space velocity output from the qp solver, $S \in \mathbb{R}^{6 \times 6}$ is the selection matrix that selects particular components of the task space velocity, $e_{6 \times 1}$ is an adjustable error term for drift compensation or frame correction.
For example, in a 6-DOF robot setting, if we want to control the end-effector to move in a straight line (aka only z-axis translation or rotation along z-axis is allowed), we can set \(b_{eq} = 0_{6 \times 1}\) and \(S = diag(1, 1, 0, 1, 1, 0)\) to deselect the x, y, and rotation components. Similarily, we can set \(S = diag(1, 1, 1, 0, 0, 0)\) and \(b_{eq} = e_{anchor}\) to lock all translation but allow rotation around the anchor point. In the other words, a software remote center of motion.
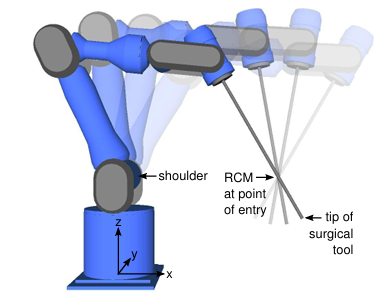
(Remote center of motion illustration. Source: [2])
Inequality Constraints
The inequality constrains are used to for self-collision avoidance by modeling the robot as a set of bounding volumes (spheres and capsules) and checking the cross-over between defined pairs are always greater than the sum of their radii [3].
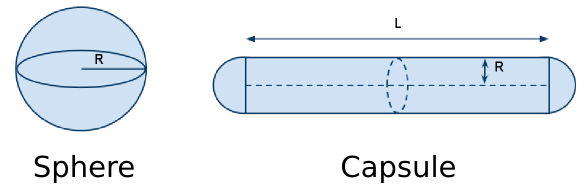
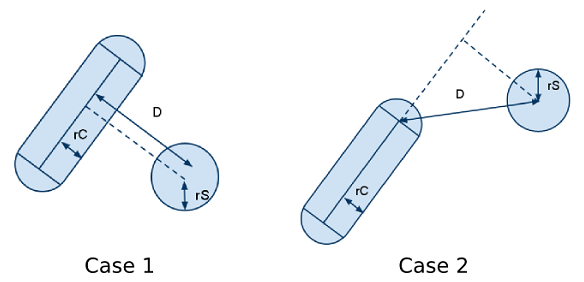
(Self-collision mesh illustration and the collision pairs. Source: [3])
The inequality constraints are then constructed as:
\[\begin{align*} d_{ij} + n_{ij}^\top (J_{p_i} - J_{p_j}) \delta t \dot{q} &\geq r_i + r_j \\ -n_{ij}^\top (J_{p_i} - J_{p_j}) \dot{q} &\leq (d - r_i - r_j) / \delta t \\ \end{align*}\]where $d_{ij}$ is shortest the distance between the pair of bounding volumes, $n_{ij}$ is the normalized directional vector, $J_{p_i}$ and $J_{p_j}$ are the Jacobian of the robot at the target frame, $\delta t$ is the time step, and $r_i$ and $r_j$ are the radii of the bounding volumes.
Other inequality constraints can be added to the optimization to incorporate other subtasks, including the spatial velocity limits, joint limits, singularity avoidance, and contact force constraint.
Video Demonstration
Lessons Learned
Optimization-based control is a powerful framework for shared-control robot design. It allows a flexible and generalizable control framework. By stacking up properly designed objective functions and linear constraints, we can design a robotic system that serve our task space mission subjected to different constraints.
References
[1] Keemink, A. Q., Van der Kooij, H., & Stienen, A. H. (2018). Admittance control for physical human–robot interaction. The International Journal of Robotics Research, 37(11), 1421-1444.
[2] Locke, R. C., & Patel, R. V. (2007, April). Optimal remote center-of-motion location for robotics-assisted minimally-invasive surgery. In Proceedings 2007 IEEE International Conference on Robotics and Automation (pp. 1900-1905). IEEE.
[3] Self-collision avoidance. NAOqi Motion. Link: https://www.bx.psu.edu/~thanh/naoqi/naoqi/motion/reflexes-collision-avoidance.html
tags: RoboticsBack to Blogs | Top | Tags